简单说说R语言做复杂中介

博主：理想家
发布时间：2025 年 01 月 16 日
62 次浏览
暂无评论
3458字数
分类：分享

# 简单说说R语言做复杂中介

前段时间（好像也挺长时间了），某期刊上的一篇文章引发了比较大的讨论，至少我是刷到了不少视频和文章讲这篇文章。这篇文章将组态分析和回归分析结合了起来，就是这文章名字听着着实唬人，我个人观点，在回归分析里面，就是一个简单、标准的中介。

## 简单中介

首先说说简单中介，相对于下面的复杂中介，那么其他的中介，都可以称为简单中介了，比如平行中介，链式中介，有调节的中介。这里放几个画的图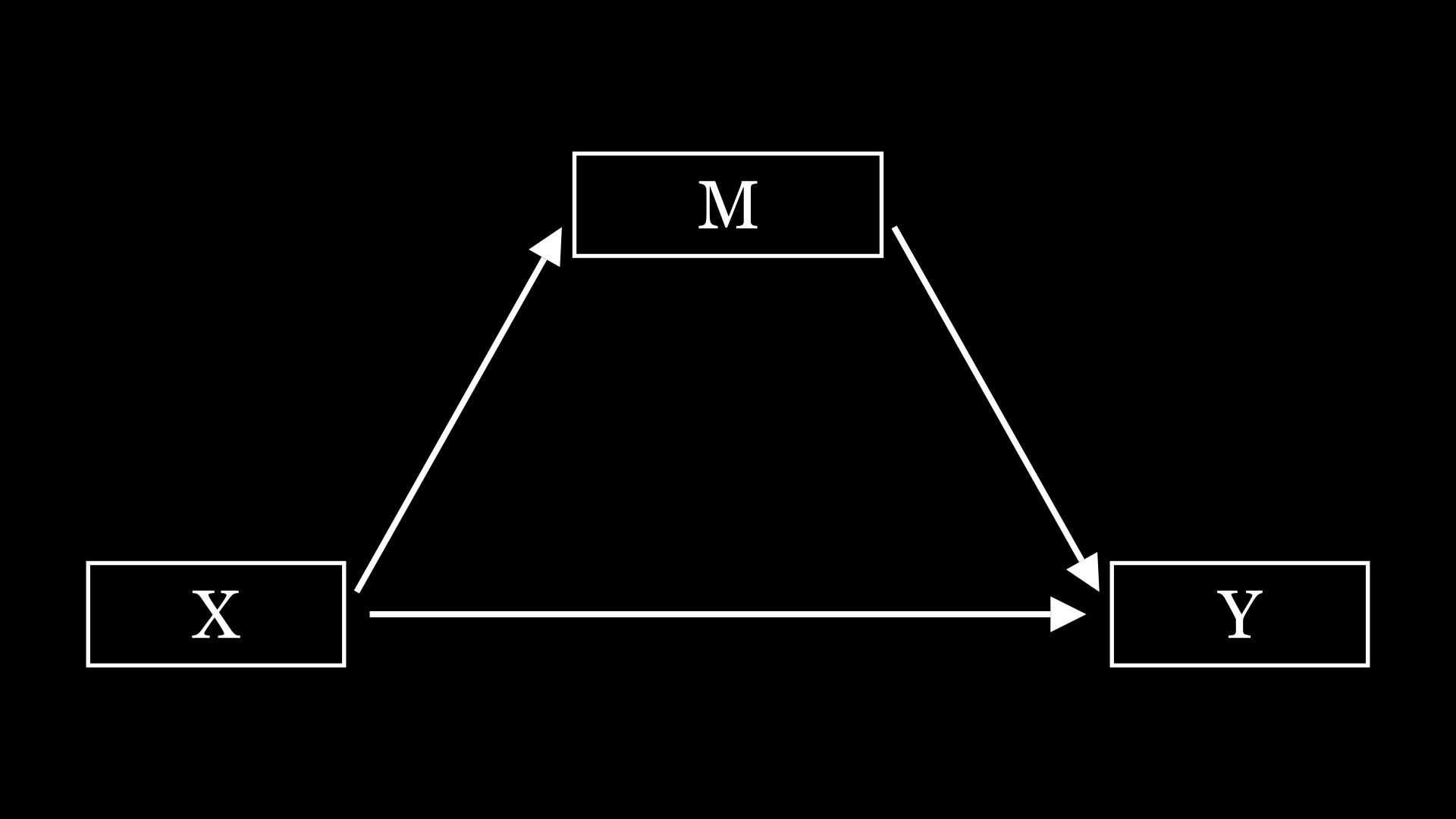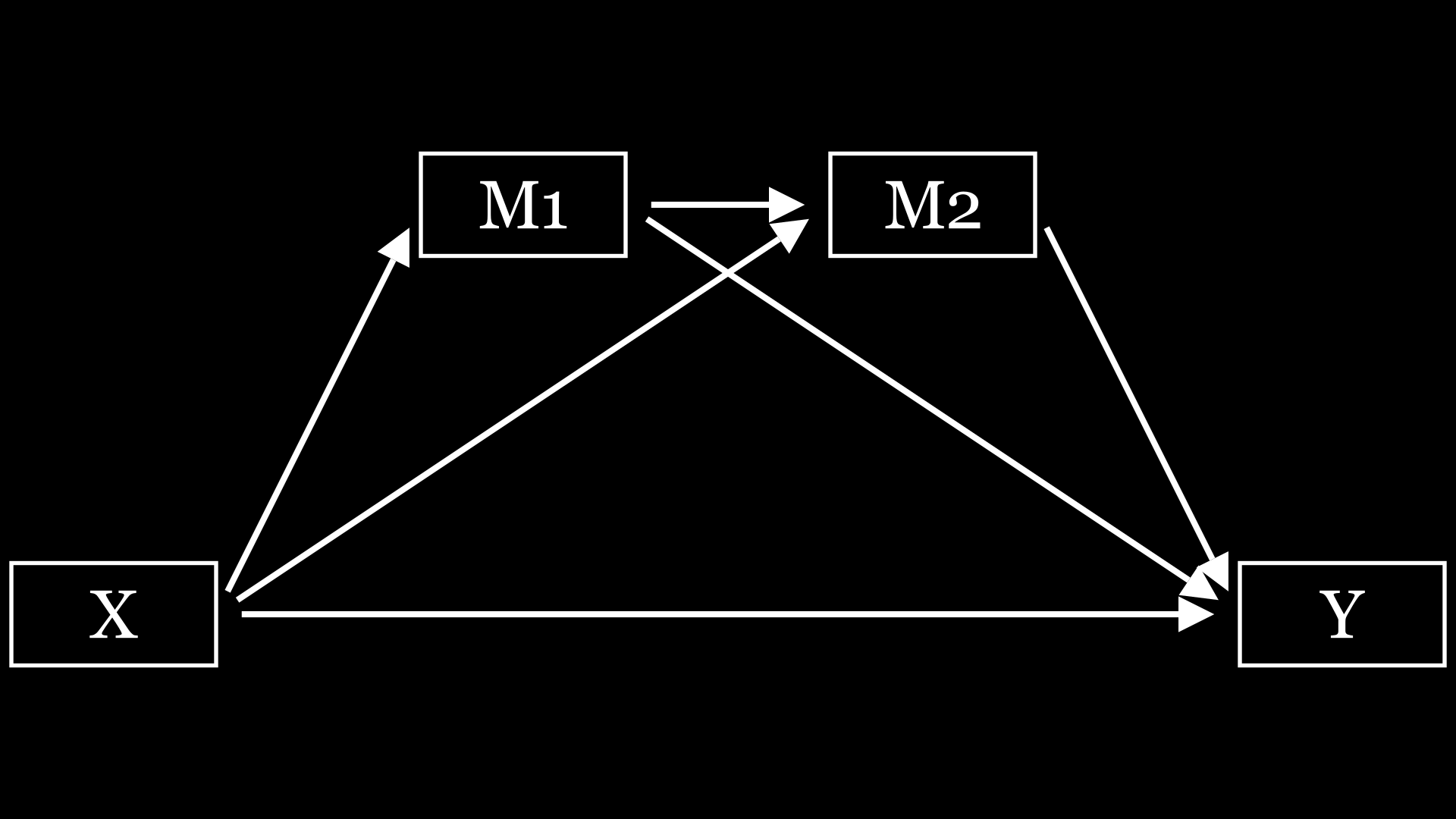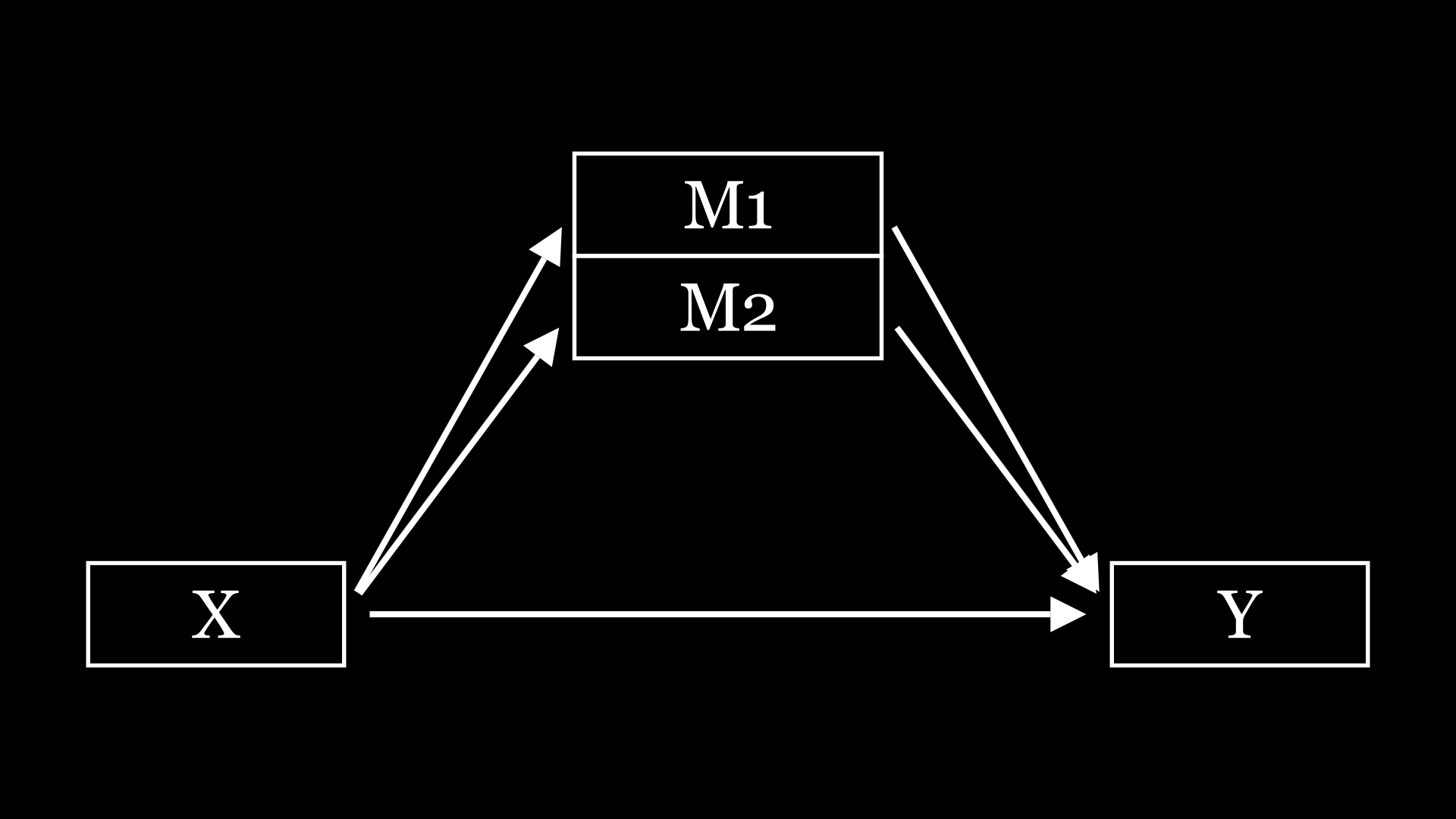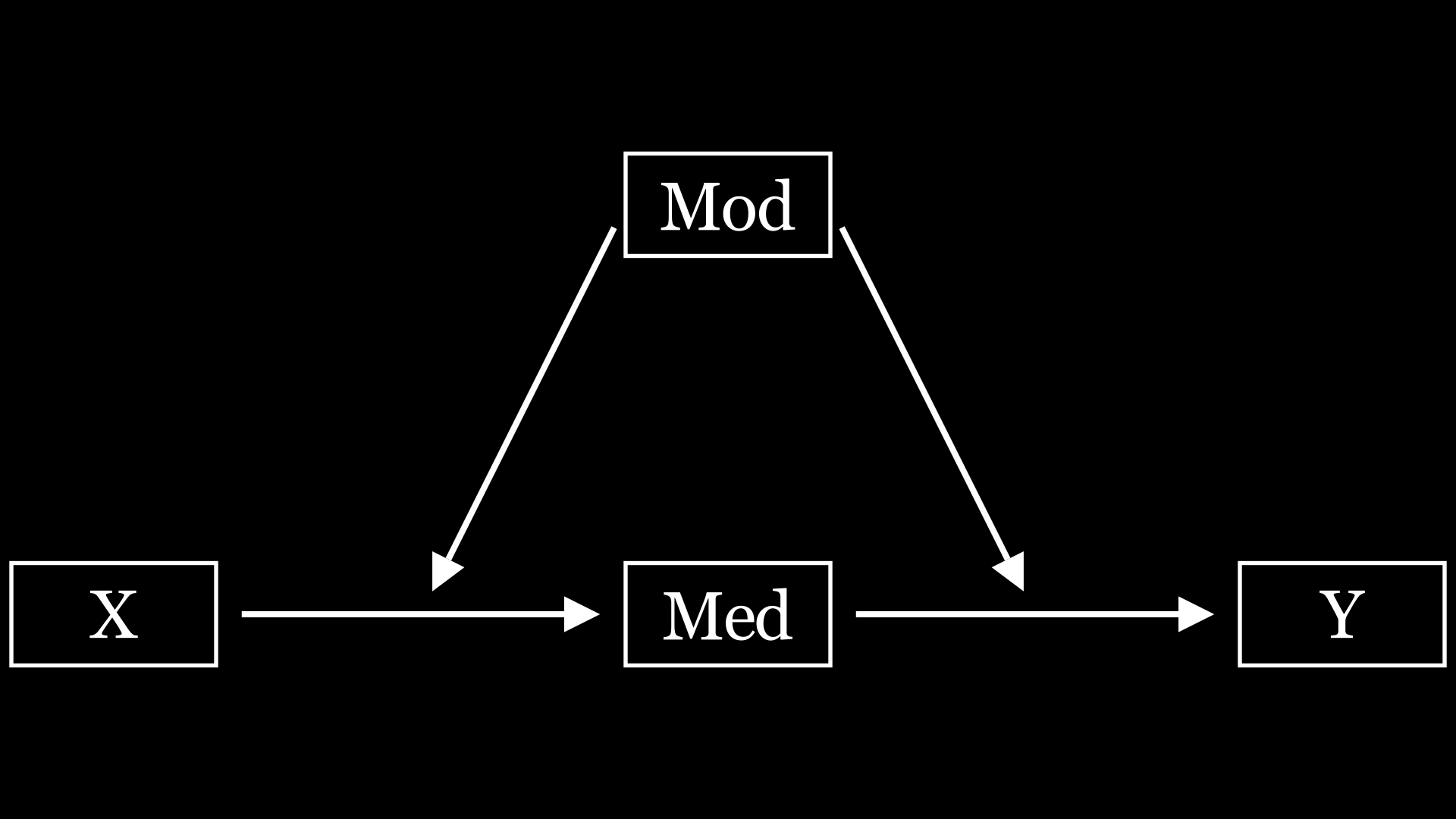

![标准的一个中介](https://blog.asenser.cn/usr/uploads/2025/01/3926808253.png)

![平行中介](https://blog.asenser.cn/usr/uploads/2025/01/2246753855.png)![链式中介](https://blog.asenser.cn/usr/uploads/2025/01/1865646757.png)

![调节中介](https://blog.asenser.cn/usr/uploads/2025/01/4183752993.png)

这些中介模型相信大家都比较熟悉了，就不多阐述了。

## 复杂中介

通过对原文的一个阅读，可知复杂中介模型是一种融合了组态视角和多种分析方法的研究工具，旨在解决传统线性中介模型在面对复杂系统问题时的局限性。原文阐述的步骤如下：

1. **检验 $X_{i} \to m$ 因果链**：通过完整的QCA分析，探究前因条件 $x_{i}$ 与中介变量 $m$ 的必要和充分两类复杂因果关系，发现驱动 $m$ 的不同组态 $X_{i}$ 。若未发现，则停止分析。此步骤基于整体论视角，利用QCA方法挖掘变量间的复杂关系，突破了传统线性分析的局限，能更好地应对复杂系统中多变量相互依赖的情况。
2. **赋值组态 $X_{i}$**
   - 计算案例在组态包含的所有相关条件中的集合隶属度。对于出现的条件，直接使用案例在该条件集合中的隶属度（通过QCA分析中的校准步骤得到）；对于不出现的条件，使用非集运算计算案例在非条件集合中的隶属度（公式为 $\sim x_{j}=1 - x_{j}$ ）。
   - 计算案例在组态 $X_{i}$ 中的集合隶属度，公式为 $mX_{i}=min(x_{1},\cdots,x_{j})$ ，即案例在组态中的隶属度是其在所有相关条件集合中隶属度的最小值。通过这一系列运算，将QCA结果转换为回归分析的自变量，为后续混合分析做准备。
3. **检验 $x \to y$ 因果链**：通过回归分析，检验驱动 $m$ 的不同组态 $X$ （自变量）与因变量 $y$ 的平均效应关系（$y = cX_{i}+e_{1}$ ），分析自变量 $X_{i}$ 对因变量的总效应 $c$ 。此步骤基于还原论视角，分析近似独立子系统层面的简单关系，与前一步骤的整体论分析形成互补，共同构建起复杂中介模型的分析框架。
4. **检验 $m \to y$ 因果链**：通过回归分析，检验控制自变量（组态 $X$ ）时，中介变量 $m$ 与因变量 $y$ 的平均效应关系（$y = c'X_{i}+bm + e_{3}$ ）。若系数 $b$ 显著，则说明 $m$ 显著影响 $y$ ，表明组态 $X_{i}$ 通过 $m$ 影响 $y$ 的间接效应存在，即 $X_{i} \to m \to y$ 的复杂中介效应存在。进一步可通过观察系数 $c'$ 判断是否存在直接效应。同时，为避免组态相关导致的多重共线性问题，可将不同组态视为自变量，依次进行独立的回归分析。

同样的，也放个图：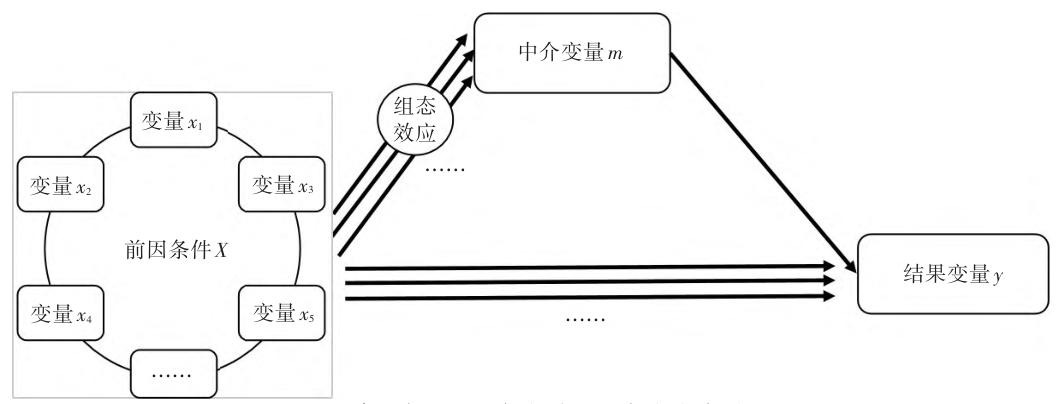

![复杂中介](https://blog.asenser.cn/usr/uploads/2025/01/2362477708.jpeg)

这里面的关键步骤就是组态的结果如何变成一个自变量，也就是第二步，赋值组态$X_i$，因为qca组态分析已经有很多资料了，大家可以自行查询一下，而回归，或者说中介，大家也十分熟悉了。

我们先来了解一下组态的结果是什么类型的、组态的结果有一个条件集合，如下面的`x1*x3*x4`是一个集合，并且每个样本在每个指标下面都有个隶属度。画一个表格来帮助理解一下：

| ID | x1  | x2  | x3  | x4  | x5  |
| -- | --- | --- | --- | --- | --- |
| 1  | 0.2 | 0.3 | 0.9 | 0.3 | 0.5 |

上面就是样本1对于每个指标的隶属度
在计算样本对于条件组态的隶属度之前，我们需要了解组态集合之间的运算关系：
OR关系(\*)：

- 取最小值原则
- 隶属度 = MIN(条件A的隶属度, 条件B的隶属度)
- 例如:如果A=0.8, B=0.6,则A\*B=0.6

AND关系(+):

- 取最大值原则
- 隶属度 = MAX(条件A的隶属度, 条件B的隶属度)
- 例如:如果A=0.8, B=0.6,则A+B=0.8

NOT关系(~):

- 取补集
- 隶属度 = 1 - 原隶属度
- 例如:如果A=0.8,则~A=0.2
  现在样本1对于条件组态`x1*x3*x4`的隶属度计算就是在x1,x2,x4中区最小值，因为组态`x1*x3*x4`里面的逻辑计算都是OR关系，即取最小值。

| ID | x1  | x2  | x3  | x4  | x5  | x1\*x3\*x4 |
| -- | --- | --- | --- | --- | --- | ---------- |
| 1  | 0.2 | 0.3 | 0.9 | 0.3 | 0.5 | 0.2        |

假设现在样本1对组态`x1*~x2*~x3*x6 `又该怎么计算嘞，一步步来。我们将组态翻译一下：
`(x1正常取)*(x2取补集)*(x3取补集)*(x6正常取)=(x1)*(1-x2)*(1-x3)*(x6)`，那么，现在就跟刚才的情况一样了。

| ID | x1  | x2  | x3  | x4  | x5  | x1\*x3\*x4              | x1\*\~x2\*\~x3\*x5                 |
| -- | --- | --- | --- | --- | --- | ----------------------- | ---------------------------------- |
| 1  | 0.2 | 0.3 | 0.4 | 0.3 | 0.5 | (0.2)\*(0.3)\*(0.3)=0.2 | (0.2)\*(1-0.9)\*(1-0.4)\*(0.5)=0.1 |

依照这个计算方法，现在每个样本对于每个条件组态都有一个值，那么现在条件组态就可以作为一个自变量了。

```txt
--- COMPLEX SOLUTION ---
frequency cutoff: 1
consistency cutoff: 0.872534
                          raw       unique          
                        coverage    coverage   consistency 
                       ----------  ----------  ----------  
x1*x3*x4               0.642248    0.0403785   0.906484  
x1*~x2*~x3*x5          0.195991    0.0159534   0.962952
```

用R语言完成这一步的代码也很简单，就不多解释了。

```r
data <- data %>% 
  mutate(
    X1=pmin(x1,x3,x4),
    X2=pmin(x1,1-x2,1-x3,x5),
  )

fit <- lm(y~X7+x1+x2,data=data)
summary(fit)
```

## 总结

将QCA和回归分析结合的复杂中介模型，感觉非常有趣！这种方法不仅能处理传统线性中介模型的局限性，还能更好地分析复杂系统中的中介效应。具体来说，先用QCA检验前因条件和中介变量的因果关系，然后通过赋值组态将其转换为回归分析的自变量，最后用回归分析检验中介效应。整个过程就像搭积木一样，把整体论和还原论的视角巧妙地结合在一起。总的来说，这种分析方式为研究复杂系统中的中介效应提供了新的思路，不得不说，这些大佬真聪明！

最后修改：2025 年 01 月 16 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

评论 *

私密评论

名称 *

🎲

邮箱 *

地址

简单说说R语言做复杂中介

理想家 • 2025 年 01 月 16 日

# 简单说说R语言做复杂中介

## 简单中介

首先说说简单中介，相对于下面的复杂中介，那么其他的中介，都可以称为简单中介了，比如平行中介，链式中介，有调节的中介。这里放几个画的图

![标准的一个中介](https://blog.asenser.cn/usr/uploads/2025/01/3926808253.png)

![平行中介](https://blog.asenser.cn/usr/uploads/2025/01/2246753855.png)![链式中介](https://blog.asenser.cn/usr/uploads/2025/01/1865646757.png)

![调节中介](https://blog.asenser.cn/usr/uploads/2025/01/4183752993.png)

这些中介模型相信大家都比较熟悉了，就不多阐述了。

## 复杂中介

同样的，也放个图：

![复杂中介](https://blog.asenser.cn/usr/uploads/2025/01/2362477708.jpeg)

| ID | x1  | x2  | x3  | x4  | x5  |
| -- | --- | --- | --- | --- | --- |
| 1  | 0.2 | 0.3 | 0.9 | 0.3 | 0.5 |

上面就是样本1对于每个指标的隶属度
在计算样本对于条件组态的隶属度之前，我们需要了解组态集合之间的运算关系：
OR关系(\*)：

- 取最小值原则
- 隶属度 = MIN(条件A的隶属度, 条件B的隶属度)
- 例如:如果A=0.8, B=0.6,则A\*B=0.6

AND关系(+):

- 取最大值原则
- 隶属度 = MAX(条件A的隶属度, 条件B的隶属度)
- 例如:如果A=0.8, B=0.6,则A+B=0.8

NOT关系(~):

| ID | x1  | x2  | x3  | x4  | x5  | x1\*x3\*x4 |
| -- | --- | --- | --- | --- | --- | ---------- |
| 1  | 0.2 | 0.3 | 0.9 | 0.3 | 0.5 | 0.2        |

依照这个计算方法，现在每个样本对于每个条件组态都有一个值，那么现在条件组态就可以作为一个自变量了。

用R语言完成这一步的代码也很简单，就不多解释了。

```r
data <- data %>% 
  mutate(
    X1=pmin(x1,x3,x4),
    X2=pmin(x1,1-x2,1-x3,x5),
  )

fit <- lm(y~X7+x1+x2,data=data)
summary(fit)
```

## 总结

简单说说R语言做复杂中介

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

旅行

欢迎使用 Typecho

PyTorch正菜-Tensor（上）

PyTorch正菜-数据读取(一)

PyTorch正菜-常用的视觉处理模型

PyTorch正菜-数据读取(一)

用R帮助你完成毕业论文实证的常规流程

PyTorch一周目（2）张量和自动微分

PyTorch一周目（4）数据预处理技巧

旅行

简单说说R语言做复杂中介

发表评论 取消回复 使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

简单说说R语言做复杂中介

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款